Epsilon. ε. The fifth letter of the Greek alphabet. In calculus, an arbitrarily small positive quantity. In formal language theory, the empty string. In the theory of computation, the empty transition of an automaton. In the ISO C Standard, 1.19e-07 for single precision and 2.22e-16 for double precision.
The other day I was attempting to use FLT_EPSILON (which I later learned was laughably incorrect) when the Swift 4 compiler emitted a warning saying that FLT_EPSILON is deprecated and to use .ulpOfOne instead. What the hell is ulpOfOne? I read the documentation and then everything made sense — ha, just kidding. The FloatingPoint.ulpOfOne docs generously describe the static variable as the unit in the last place of 1.0 — whatever that means. Let’s find out.
Update 18 April 2018
I gave a talk on the topics discussed in this post and more at iOS Conf Singapore. You can watch the video here!

Aside: new protocols in Swift 4
The various numeric protocols got a facelift in Swift 4 (as well as in Swift 3). There’s a new, top-level Numeric protocol, some new integer proposals, numerous API additions to the FloatingPoint protocol (including ulpOfOne), as well as additions to the other numeric protocols.
Relevant Swift Evolution proposals:
- SE-0104: Protocol-oriented integers (Swift 4)
- SE-0113: Add integral rounding functions to FloatingPoint (Swift 3)
- SE-0067: Enhanced Floating Point Protocols (Swift 3)
ulpOfOne and ulp
The discussion section for .ulpOfOne elaborates a bit more:
The positive difference between
1.0and the next greater representable number. TheulpOfOneconstant corresponds to the C macrosFLT_EPSILON,DBL_EPSILON, and others with a similar purpose.
There’s also a computed property for Swift FloatingPoint protocol conformers called ulp. It’s a property, so you can write something like 1.0.ulp or 3.14159.ulp. According to the documentation, ulp is the unit in the last place of this value. So, it’s the same as .ulpOfOne but for any value. The discussion section explains:
This is the unit of the least significant digit in this value’s significand. For most numbers x, this is the difference between x and the next greater (in magnitude) representable number. There are some edge cases to be aware of […]
This quantity, or a related quantity, is sometimes called epsilon or machine epsilon. Avoid that name because it has different meanings in different languages, which can lead to confusion, and because it suggests that it is a good tolerance to use for comparisons, which it almost never is.
For most numbers x, this is the difference between x and the next greater (in magnitude) representable number. This makes more sense — floating-point numbers are difficult to represent in computing because they are inherently imprecise due to rounding. Given the above, it’s clear why FLT_EPSILON is not intended to be used as a tolerance for comparisons. I’ll blame the terrible naming for my mistake there. 😉
As Olivier Halligon pointed out to me, there are additional details in the header docs:
NOTE: Rationale for “ulp” instead of “epsilon”: We do not use that name because it is ambiguous at best and misleading at worst:
Historically several definitions of “machine epsilon” have commonly been used, which differ by up to a factor of two or so. By contrast “ulp” is a term with a specific unambiguous definition.
Some languages have used “epsilon” to refer to wildly different values, such as
leastNonzeroMagnitude.Inexperienced users often believe that “epsilon” should be used as a tolerance for floating-point comparisons, because of the name. It is nearly always the wrong value to use for this purpose.
By contrast “ulp” is a term with a specific unambiguous definition. I’m not sure who wrote that, but “unambiguous” is a term I’d rarely use to describe anything regarding naming in computer science and programming. 😆 ULP is short for Unit in the Last Place, or Unit of Least Precision. It’s a unit, but what does it measure? It measures the distance from a value to the next representable value.
Why we need ulp
Consider integer values which can be represented exactly in binary. The distance from 0 to 1 is 1, the distance from 1 to 2 is 1, and so on. In fact, it’s always 1 — the distance between integers is uniform across all representable values and precisely equal to 1. In other words, for any value the next representable value is 1 away. This is intuitive if you imagine a number line with only integer values. We do not need any notion of “ulp” for integers. They are simple and easy to represent in a base-2 number system.
Floating-point numbers, however, are more complex and difficult to represent in bits. In Number theory, this is the set of real numbers R, which includes the irrational numbers R/Q, the rationals Q, the integers Z, and the natural numbers N. Basically, all the numbers. 😆 While the set of all real numbers is uncountably infinite, the set of all rational numbers is countable, which means that almost all real numbers are irrational. Irrational numbers never terminate, so obviously need to be rounded. What’s more critical is that the rational numbers are densely ordered — for any two rational numbers there are infinitely many between them. In fact, there are more numbers (R/Q + Q) between 0 and 1 than there are in the entire set of integers Z.
Computers obviously cannot represent all of the integers — from negative to positive infinity — which is why we have INT_MIN, INT_MAX, and other constants. Similarly, floating-point numbers are bound by FLT_MIN and FLT_MAX (or DBL_MIN and DBL_MAX). But more importantly, computers cannot represent all of the rational and irrational numbers between these bounds. While the representable integers are countable within their specified bounds of INT_MIN and INT_MAX, the floating-point numbers that occur between FLT_MIN and FLT_MAX are infinite. It’s clear that we need some kind of rounding mechanism, which means not all numbers are representable. Such a rounding mechanism will provide a way to determine the distance from one value to the next representable value — or, ulp. Thus, aside from the obvious limitations of silicon chips, this is why ulp needs to exist.

Memory layout of floating-point numbers
Before we define ulp, let’s briefly review the memory layout for floating-point numbers.
First, integers are exact and can be represented directly in binary format. Signed integers are typically represented in two’s complement, but that’s an implementation detail. Conceptually, you have an integer which is stored as some bits. For example, 6 which is 0b0110. Floating-point numbers have three components: a sign, an exponent (which is biased), and a significand. For single precision, there’s 1 bit for the sign, 8 bits for the exponent, and 23 bits for the significand — 32 bits total. Double precision provides 11 bits for the exponent and 52 bits for the significand, which totals 64 bits. I won’t discuss the more elaborate details about how floating-point numbers work in this post, but you’ll find additional reading at the end.
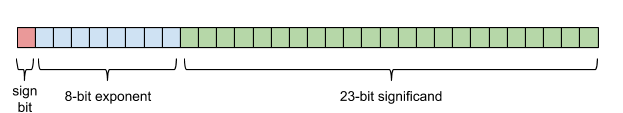
IEEE 754 single-precision binary floating-point format / Source
Note that with this representation, positive and negative zero (+0 and -0) are two distinct values, though they compare as equal. If you ever wondered why computers have signed zero, this is why.
Let’s look at an example in base-10. We can represent 123.45 with a significand of 12345 and exponent of -2: 123.45 = 12345 * 10e−2. In base-2, computing a value from these three components is a bit more complicated but conceptually the same. Swift provides a clear and expressive API that can really help us understand how all of this works.
let value = Float(0.15625) // 1/8 + 1/32
value.sign // plus
value.exponent // -3
value.significand // 1.25
We can recompute the decimal value from its component parts. Note that the radix, or base, is 2 — as in base-2 for binary.
// significand * 2^exponent
Float(value.significand) * powf(Float(Float.radix), Float(value.exponent))
// 0.15625
Additionally, Swift’s APIs allow us to explore the memory layout. We can look at the bit patterns and verify them with this handy IEEE-754 floating-point converter.
// 0.15625
value.exponentBitPattern // 124
value.significandBitPattern // 2097152
We can also check the bit counts for each component:
Float.exponentBitCount // 8, bits for the exponent
Float.significandBitCount // 23, bits for the significand
Double.exponentBitCount // 11, bits for the exponent
Double.significandBitCount // 52, bits for the significand
Defining ulp
Surprisingly, the IEEE standard doesn’t define ulpOfOne (or machine epsilon) explicitly, so there are a couple of varying definitions. However, most standard libraries provide constants for these values. The most prevalent is the ISO C Standard — 1.19e-07 for 32-bit values (Float) and 2.22e-16 for 64-bit values (Double). As expected, this is what we see in Swift:
Float.ulpOfOne
// 1.192093e-07, or
// 0.00000011920928955078125
Double.ulpOfOne
// 2.220446049250313e-16, or
// 0.00000000000000022204460492503130808472633361816406250
Given these initial epsilon or ulpOfOne values, we can compute the ulp for any value v with an exponent exp as: epsilon * 2^exp, where 2 is the radix, or base.
let value = Float(3.14)
let ulpOfValue = Float.ulpOfOne * powf(2.0, Float(value.exponent))
ulpOfValue // 0.00000023841857910156250
value.ulp // 0.00000023841857910156250
Again, Swift provides a great, readable API for manipulating and exploring the properties of floating-point values. For example, for any value we can check .nextUp to see the next representable value. Given what we’ve learned so far, we can intuitively reason about what the next number (.nextUp) must be and verify our result.
let value = Float(1.0)
value.ulp // 0.00000011920928955078125
value + value.ulp // 1.00000011920928955078125
value.nextUp // 1.00000011920928955078125
let value = Float(1_000.0)
value.ulp // 0.00006103515625000000000
value + value.ulp // 1000.00006103515625000000000
value.nextUp // 1000.00006103515625000000000
let value = Float(3.14)
// actually 3.14000010490417480468750 -- because rounding
value // 3.14000010490417480468750
value.ulp // 0.00000023841857910156250
value + value.ulp // 3.14000034332275390625000
value.nextUp // 3.14000034332275390625000
Notice that the ulp of 1 is not the same as the ulp of 1,000. For each floating-point number ulp varies. In fact, the precision of a floating-point value is proportional to its magnitude. The larger a value, the less precise.
let value = Float(1_000_000_000.0)
value.ulp // 64.0
value.nextUp // 1000000064.0
Viewing the source
We can view the Swift standard library source, which lives in stdlib/public/core/ FloatingPointTypes.swift.gyb. If you’ve never seen .gyb (‘generate your boilerplate’) files, read Ole Begemann’s post. Per Ole’s instructions, we can generate the specific implementation for Float.
public var ulp: Float {
if !isFinite { return Float.nan }
if exponentBitPattern > UInt(Float.significandBitCount) {
// self is large enough that self.ulp is normal, so we just compute its
// exponent and construct it with a significand of zero.
let ulpExponent =
exponentBitPattern - UInt(Float.significandBitCount)
return Float(sign: .plus,
exponentBitPattern: ulpExponent,
significandBitPattern: 0)
}
if exponentBitPattern >= 1 {
// self is normal but ulp is subnormal.
let ulpShift = UInt32(exponentBitPattern - 1)
return Float(sign: .plus,
exponentBitPattern: 0,
significandBitPattern: 1 &<< ulpShift)
}
return Float(sign: .plus,
exponentBitPattern: 0,
significandBitPattern: 1)
}
Surprising at an initial glance, this is not the simple formula noted above (epsilon * 2^exponent). First there are some edge cases to handle, like Float.nan.ulp which is nan. Then it constructs a new Float after computing its constituent components — the sign, exponent, and significand. This code eventually calls into the public initializer: init(sign: exponentBitPattern: significandBitPattern:). Note that the final return is equivalent to Float.leastNonzeroMagnitude (or FLT_MIN).
We can view the implementation of this initializer. We see a lot of bit manipulation, namely bitwise AND (&) and masking left shift (&<<).
public init(sign: FloatingPointSign,
exponentBitPattern: UInt,
significandBitPattern: UInt32) {
let signShift = Float.significandBitCount + Float.exponentBitCount
let sign = UInt32(sign == .minus ? 1 : 0)
let exponent = UInt32(
exponentBitPattern & Float._infinityExponent)
let significand = UInt32(
significandBitPattern & Float._significandMask)
self.init(bitPattern:
sign &<< UInt32(signShift) |
exponent &<< UInt32(Float.significandBitCount) |
significand)
}
This initializer eventually calls into init(bitPattern:), where it finally constructs a primitive LLVM 32-bit float (FPIEEE32) from the raw bit pattern.
public init(bitPattern: UInt32) {
self.init(_bits: Builtin.bitcast_Int32_FPIEEE32(bitPattern._value))
}
We can break this down and observe each step in a Swift playground. For private APIs like Float._infinityExponent, we can look at the source and define them inline.
// starting value
let value = Float(3.1415)
// 1. the first if is satisfied:
// var ulp: Float {
// if exponentBitPattern > UInt(Float.significandBitCount) {
let ulpSign = FloatingPointSign.plus // plus
let ulpExponent = value.exponentBitPattern - UInt(Float.significandBitCount) // 105
let ulpSignificandBitPattern = UInt32(0) // 0
// 2. we call init with the 3 values above:
// init(sign: FloatingPointSign,
// exponentBitPattern: UInt,
// significandBitPattern: UInt32) {
let signShift = Float.significandBitCount + Float.exponentBitCount // 31
let sign = UInt32(ulpSign == .minus ? 1 : 0) // 0
let _infinityExponent = 1 &<< UInt(Float.exponentBitCount) - 1 // 255
let exponent = UInt32(ulpExponent & _infinityExponent) // 105, or 2^-22
let _significandMask = 1 &<< UInt32(Float.significandBitCount) - 1 // 8388607
let significand = UInt32(ulpSignificandBitPattern & _significandMask) // 0
let signMaskLeftShift = sign &<< UInt32(signShift) // 0
let exponentMaskLeftShift = exponent &<< UInt32(Float.significandBitCount) // 880803840
let bitPattern = signMaskLeftShift | exponentMaskLeftShift | significand // 880803840
// 880803840 in binary is 00110100100000000000000000000000
// Sign Exponent Significand
// [0] [01101001] [00000000000000000000000]
// 3. initialize with the computed bit pattern
let finalUlp = Float(bitPattern: bitPattern) // 2.384186e-07, or 0.00000023841857910156250
This code is admittedly quite difficult to follow, but suffice to say it is equivalent to what we originally computed above.
let value = Float(3.1415)
let computedUlp = Float.ulpOfOne * powf(Float(Float.radix), Float(value.exponent))
value // 3.14149999618530273437500
computedUlp // 0.00000023841857910156250
value.ulp // 0.00000023841857910156250
Conclusion
So that’s ulp. There’s still a lot to unpack here. I’ve skipped over some details, but this rabbit hole gets deeper and deeper — and I had to end this post somewhere. Hopefully this was helpful to better understand ulp and a little about floating-point precision. To see how far the rabbit hole of floating-point numbers goes, check out the links below.
If I got anything wrong, please let me know or open an issue! 😅
Further reading and resources
- Comparing Floating Point Numbers, 2012 Edition, Bruce Dawson
- Floating Point Demystified, Part 1, Josh Haberman
- What Every Computer Scientist Should Know About Floating-Point Arithmetic, David Goldberg
- Floating Point Visually Explained, Fabien Sanglard
- Lecture Notes on the Status of IEEE 754, Prof. W. Kahan, UC Berkeley
- IEEE-754 Floating Point Converter
Update 03 April 2023
I recently discovered Xiaodi Wu’s excellent series of articles, Notes on numerics in Swift, which were written in 2018-2019. If you want to dive deeper into Swift’s numerics, I highly recommend reading these!